【4STEP解答の解説】『数B数列』153～249,演習問題19～28の解説の解説

高校数学４STEP数学Bの解説の解説

４STEP数Bの数列の解説です。不明なところは適当にコメントしてもらえると加筆します。

153

ｎに数字代入したらおわり。重要でも何でもない。

154

差がどうなってるかな～とか、何か同じもんかけてるかな～　とか見ていくだけ。　これも数列が進んでくると勝手にできるようになってるので、全く重要でない。

155

これはクソ問題。

後半にΣ（シグマ）が絡んでくるんで、その練習に今のうちにkの練習をしよ～(^^♪　

とか著者が思ったんだろうけど、こんな等差数列も等比数列もあんま馴染んでない時期にしょーもないことをして学生を混乱させるクソ問題。

後々勝手に馴染んでくるのでこの問題は無視してくれてよい。

やるんであれば、数字が変わっていってるところをkで表す感じ。

156

これは基本。等差数列って言ってるんで適当に差を求めて推測するだけ。

157

超重要問題。等差数列の一般項を求める練習。この問題は馴染むまでアホみたいに繰り返してやるべし、な問題。

158

これも重要。結局、初項と公差を求めなさい、という問題。　それがわかれば↑の157と同じ。

一般項求めた後に、ｎに10入れたら終わり。

159

これも重要。レベル低めの大学で数学Ｂが入試科目にあるところだと、こういう問題は出てきやすい。。

等差数列の一般項　　をいろんな角度からいじる問題。わかってる部分を埋めていって連立方程式で出す、みたいな展開は多い。

160

これも159と同じ。

等差数列の一般項  のわかる部分を代入→あとは連立。

161

なんかを  。　その次のやつを  と表すのが数列。

なので、 を求めてみて、　単なる数字になってしまったら、差が等しい、と言えてしまう。。。

差が等しい数列ってことは等差数列っすね。。

162

順番にならんでるやつが等差数列ってことは、

 と  が同じってことじゃないっすか？　ってことで  を計算して

 を解いて終わり。

163

超重要問題。

等差数列の和の公式  に馴染むための問題。　アホみたいに繰り返して馴染もう。 

必要なものを３つ。　初項、ｎ、末項。

164

↑の163とほぼ同じ。

いるものは初項、ｎ、末項なので、それがわかるようにいじる。

(1) (2)ともに

初項、ｎ、はわかってるの末項が分かればよい。　末項は一般項。。。

165

やっぱりいるものは、初項、ｎ、末項。

見た感じ、初項、末項はすぐわかる。ｎが知りたいところ。。　初項、公差はわかるので、一般項  を出して、90が第何項なのか調べる。。。

166

(1)(2)

なんだかんだで結局、いるものは３つ。　初項、ｎ、末項。

等差数列出す　→　初項、ｎ、末項求める　→　和の公式に入れる　→　完了

数列全般に言えることだが、よくわからなくなったら具体的な数字を並べて検証する。

7, 13, 25, 31, 37, 43 ….. 的な感じに。

(3)

全部から前の問題の分を引く、というありがちなやつ。。この展開はちょいちょい出てくるので覚えておきたい。

167

(1)(2)

文系数学のそんな偏差値高くない大学で見かけそうな問題。

やっぱ一般項  出しといて、適当にｎ入れて調べていけばいい。

168

(1) 161と同じ。 を調べてみて固定してたら等差っすね。。

(2)具体的に数字並べといて、２つ飛ばしで並べて等差数列を作ればよい。

具体例から示すのはなかなか無理があるので一応答え見とこか、ぐらいで。

「示せ」のやつはぶっちゃけあんま必要ない問題。文系数学でも理系数学でも入試で出てこない。。労力とリターンが合ってないのでスルー気味にやるのがおすすめ。

169

等差数列なら～　とか言ってるんで等差数列の一般項  をいじろっかな～と考える。

いじってって等差数列の形になれば勝ち。

170

式で表して、等差数列なので～　ってやれば終わる。

特に迷うようなものはなさそう。。

171

逆数にしたら等差数列です。　ってな問題。

あんま重要でもない。この先の問題とかやり込んでいったらいつのまにかできるようになるので、この問題が初見の場合はそこまでこだわる必要はない。

172

これは重要。

等差数列の一般項と等差数列の和の公式をちゃんとわかってんのか？

というのを確認するよい問題。

こういう問題をとーとつに出されてちゃんと解けるってのが重要。

MARCH以上を狙うなら、あたりまえにできとかなあかん問題。

173

さ～( ￣−￣)

とかなりそうやけど、

聞いてることはしょせんは等差数列の和なので、

初項、項数、末項の３つがわかったら勝ち♪

174

とりあえず一般項出す。

(1)nを入れていって探していったら終わり。

(2)項がマイナスになってると、それをたすと減るので、項がマイナスになるぎりぎり手前までを足せば和が最大になる。

175

数Aっぽい。

この問題の解答はなかなかわかりやすいので解説は不要かな。

176

しょせんは等差数列なので一般項を出す。

あとは適当に調べていって終わり。

177

初見では厳しい問題。

こういう問題をいきなりガチで取りかかってはいけない。

もれなくハマって軽く数時間無駄にしてしまう。

なので素直に答えを見て、へ～　って感じにやるのがBetter。　ネタとして知っておく、ぐらいな気持ちで。

178

これも高校生的には初見で解くのは厳しいので、とっとと答えを見る。

ただ、このネタ的なものはけっこういろんなとこに応用されてるので覚えとくといい。

部分的に素材作っといて、それらを組み合わせて答えの方に持っていく、って流れはおおい。

179

それぞれ一般項を出せるので、書き並べておわり。

例題の別解のようにやるのが手っ取り早い。

180

ま～基本。

適当になにかけたら次のんになるかな～と考える。

181

等比数列といえば、

初項と公比。

この２つがわかれば勝ち。

初項って・・・　見た瞬間わかるやん( ￣−￣)

公比は、ちょっと眺めてればわかる。

あ～２かけてるな～とか、 かけてるな～　とかを読み取る。。

182

とりあえず一般項を出す。

(1)出したら項数代入。

(2)4096になるnを探す。

183

わかってる部分で式を作る。

これはふつうに解答がわかりやすい。

184

連続してる３つが等比数列ってことは

小×大＝真ん中の２乗。

185

ふつうに等比数列の和の公式に代入しておわり。

186

とりあえず一般項出す。

末項からｎがわかる。

187

とりあえず一般項出す。

見た目から初項わかる。　眺めてれば公比もわかる。

あとは和の公式に入れておわり。

188

連続３項の等差数列の関係式（小＋大＝２中）、

等比数列の関係式（小×大＝真ん中の２乗）

を使って連立しておわり。

189

３つの実数。。。　→　a, b, c とおくか( ￣−￣)

和が１９。。。→ a+b+c=19

積が216。。。→abc=216

等比数列らしいので、　ac=ｂの２乗

あとは適当に連立しておわり。

190

等比数列つくってみて、９５４がありかなしかみる。。

等比数列つくってみて、９５４がありかなしかみる。。

191

これはアホ問題。

ここでやる必要はない。数列の組み合わせ系の問題はいっぱいあるけど、なぜこのタイミングでこれをここに入れる？

数列の他のとこもやって総合的な実力をつけてからやるっしょ。。

192

数列はいろいろ組み合わせた問題は多くなるけども、これはふつうに必要。。

とりあえずこんな感じに組み合わせますよ～　的な感じ。

193

初項、公比、和の公式、をちゃんと使いこなせんのか？　っていう問題。　ま～ふつうに必要。

194

これも等比数列で適当に式つくって解いてくださいねってな問題。ま～必要。

195

これも↑の194と同じ系統。等比数列の一般項、和の公式を使いこなしましょうってな問題。

196

(前半) 適当に代入してたら勝手に終わってる。

(後半) 和の公式作ってから適当に数字代入してたら勝手に終わる。

ただこのｎをあてる系統の問題は文系数学の入試でもよく出てくる。

197

上でも書いたけどlogは十分馴染んだあとやってば( ￣−￣)　数列にあんま馴染んでないうちにいろいろ融合問題を出すのは、初心者が凹む原因になるだけ。

198

MARCH以上とか狙うならまあまあまじめにやっといた方がいい問題。

例題になってるやつは意外と重要、かつ難しめ。

知っとくと入試で便利な技として、「小さい数で実験♪」というのがあるので、この問題の前の例題でも８００とかではなく２０とかで、ほんまに例題の言う通りになってるのか確かめる。。

199

ぱっと見よくわからない系の問題には「とりあえずやれることをやる」というのが有効。S出してみる。　T出してみる。　適当に組み合わせてみる。。　→　あ～なるほど。。　的な展開は多い。　これも上位の大学を目指すならやっといた方がいい。

200

どっかの国立大で出されてそうな問題。上位の大学を目指してて、初めて数列学習中なら、「ほほ～そういうやり方で解くのか～( ￣−￣)」　ぐらいの感じで参考にするとよい。　この問題で出てきてる展開は大学入試でよく使うものばかり。

201

ま、一応見とくか( ￣−￣)　ぐらいの問題。　

202

これも201の応用みたいなもんなんで、ほほ～( ￣−￣)　ぐらいの感じで見とく。　初見でできるわけない。

203

こういうやつの答えをサクッと出せる公式みたいなもんがありますよ♪　的なもんで、まじめに２乗とか３乗してたしている場合ではない。。。

204

(1) ｋに１入れたやつ、　ｋに２入れたやつ、と順番にたしていく。

(2) これは３から始まって１０で終わってるので、kに3を代入したやつから、kに10入れたやつまでをたす。

205

この辺はぶっちゃけどうでもええ。　Σ(シグマ)に慣れてくれば勝手にできるようになる。

とりあえずΣをやり始めた時期としては、

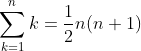
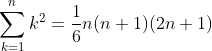
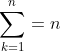
をとっとと暗記して頭に叩き込んどきたいところ。

206

これはふつーに重要。

上の３つの練習。　それと重要なのが、

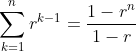
↑これ。

これは公式というよりは、初項１の等比数列の和として処理する。。

(3)は　k-1乗になおしてからさばく。

等比数列っすよ！感をしっかり出してからやるとハマりにくい。

207

これはふつーに重要。　つかシグマの練習といえばこれ。

これをなんも見ずにできるようになるまでやり込もう。

(4)　は等比数列の形 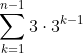にしてからやっとくといい。

208

右みたらやること書いてくれてる。。。　それそのまま使ってｎ→ｋにしといてシグマ計算して終わり。

ちなみにｋは入れもんみたいなもん。　ｋに１入れて、２入れて、３入れて・・・、ｎ入れて・・で全部たす。

なのでいきなりｎのまま使ったらマズい。　最後だけか？( ￣−￣)　みたいになる。

209

一般項の時点で和になってるパターンのやつ。。

一般項で和なことは和やけど、さらにそれの和を求めろとか言われてるんでしゃーなしに和を求める公式をかます。。

(1)はそのまま当てはめるだけ。

(2)は等比数列の和にさらにΣをかますはめになるけど、意外にたいしたことはない。。

210

これはめちゃめちゃ重要。文系で日東駒専とか狙うにしても重要。

階差数列だしといて、もとの数列の一般項を求めるごくごく基本的な問題。。

でも、多くの学生は数列のここまででいろいろおろそかにしてやってきたので、階差数列とか言われてもよくわからん、ってことが多い。

なのでこの症状が出てしまった場合は、この前までの数列がいまいち馴染んでない可能性が高いので戻ろう。。

あと、とりあえず慣れることも必要なので

のイメージでやればいい。とりあえず計算に慣れてしまうこともかなり重要。

ただ記述のときは、

とか言って突っ込んでくるので定期テストとかでは注意。

数学教師はふつーにキモいものの、n=1なら本来、

であるはずの階差数列が、

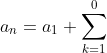
ってなって、

第１項から第０項までたす、とかなってエラいことになる・・・( ￣−￣)

なので階差数列をかますときはいつも

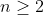
のとき、　っていう感じにn=1だけ外しておく。。

でないともれなく、

ってなっておわる。。

高校生は繊細なので、数学教師にこんなごねられ方されただけで数学嫌いになったりしかねないのでかなり危険。

で最後にn=1を検証してみて、結局n=1でもよかったですね♪　的な確認をする。。だから解答がそんな風になっている。。

ま～ほぼほぼn=1でもいけるんやけど。。。

211

これは公式っぽいもん

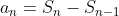
にそのまま代入して終わり。

ただ、記述するときは、いきなり代入して答えだけ出したら死ぬ。

だいたい数学の先生ってのは基本キモいんで、

的な話になって減点される。　ま～たしかに、

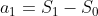
こうなってしまうのでエスゼロってなに？( ￣−￣) とはなる。。

なので解答みたいな感じになる。

一応n=1のときも調べてみたら、出てきた答えと一緒なんで、じゃ～それで♪　みたいな感じ。

212

公式に代入しただけ。

ただ、lとかmとか使ってるのでその辺には見慣れておきたい。

kが使えなくなるから仕方なく別の文字使ってるだけ。　たいした意味はない。

213

なんじゃこれ( ￣−￣)　となる問題。　ただ、ぶっちゃけたいしたことはない。

そもそもこんな風に数列を羅列してくれてるやつは、1,2,3,4,てなっていってるところはkとおける。

(1)　だから(1)はkとk+1使ってるな～( ￣−￣)　で終わってまう。。。　あとはΣっておわり。

(2)　奇数の２乗の和っすね。。　ってなるが、なにげに書き方がわかりにくいのでしゃーなしに答え見て、あ～そう書くのね( ￣−￣)　と理解する。

和を求めといて、さらに和をかますってのはそろそろ常套手段。。

214

213と同じような雰囲気。

(1) 1,3,5,7,ってことはkでいけば、2k-1やな～とすぐにわかる。

後半部分は、nからｈとつずつ下がってきてるものの、kで言えば0,1,2,3,4,5,　なので、

(n+1 -k) としてみる。　これでk=1,2,3,4,5って入れていって検証してみる。。。　すると、

あってるやん( ￣−￣)　となるので、組み合わせておわり。

(2) ぶっちゃけ(1)ができれば(2)もできる。

（n+1 -k) のところがわかってれば問題ない。なにも変わらない。全く同じ問題といってしまってもいいぐらい。

くれぐれも解答を見て、(n-k+1)というのを見て憤りを感じないように。

たまたまそう置いてみたらうまく説明できたので使ってるだけ。

４STEPの解答がクソであることがよくわかる良問。

215

ってなる問題。

それさえわかってしまえばあとは丁寧に計算していけばいい。くれぐれもどれの初項がどれかには気をつける。。

216

初見だと厳しい問題。

ただ211とやり方的にはあんまりかわらん。

ほほ～( ￣−￣)　と解答でも見とくのがよい。

217

これはアホみたいに重要。分数をバラす、部分分数分解の練習問題。

やりかた自体はたいしたことはない。

文系数学でよく出てくる問題。

218

217と方向性は同じ。

こういうルートを見たらだいたい有理化すると思っておくとよい。

あとは初項から適当に並べといてバシバシ消す。

219

これは初見ではかなり厳しい問題。

素直に解答をみて、ほほ～( ￣−￣)　と学習しておく。

220

等差数列×等比数列 の場合は 全体に公比をかけたやつを連立みたいに引く、と解説に書けってば。。( ￣−￣)

このタイプのやつはこの倒し方って決まってるんで、　生のやつと公比かけたやつをひっ算して引くだけ。

あとは解答みたいに解けばいい。。。

221　群数列

これはクソほど重要なやつ。かつ苦手としている学生が多いやつ。。。　いろんな解き方があるので適当に好きなようにやればいい。　ただ、

というところには気をつけたい。

(1) これ、4STEPの解答、解答になっとるか？( ￣−￣)

第ｎ群の最初の自然数は・・・　それだけ取り出して、

1 | 2 | 4 | 8 | 16 | ・・・・　ってなる。。。

これ、ふつーに初項１公比２の等比数列やん( ￣−￣)　

(2)とりま、近くまでいく。

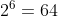
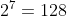
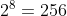
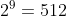
なので、試しにn=10 にしてみると、(1)の結果を使って、10群の最初の数は512となる。。　ということで10群は行き過ぎている。。

ということで、500は第９群確定♪

10群と9群の境目付近を書いてみると、

|・・・・499, 500, 501, 502, 503, 504, 505, 506, 507, 508, 509, 510, 511 | 512, 513, 514, 515,・・・・・・・

となる。。。

ということで第9群のうしろから11番目。　ってことやけど前からは？( ￣−￣)　ってなるんで

よく問題みてみりゃ第n群には個の項があるらしいので、9群には256項ある。

500を245番目としてみると、246，247，248と数えていけばちょうど最後の511が256番目になる♪

ということで500は第9群の245番目。

(3) これはネタを知ってるとそんなにむずくはない。

全体的には等差数列なので、和が知りたければ、初項、項数、末項　がわかればいい。

n群の最初は

n群の項数は

n群の最後は？・・・( ￣−￣)

ってとこやけど、(n+1)群の最初から1ひいたやつがn群の最後。。なので

n群の最後は

ということで、あとは等差数列の和の公式みたいなやつに入れておわり。

群数列はいろんなとこで出てくるので慣れておきたい。

222

(1)縦に並べるのもあり。

1

1,4

1,4,9

1,4,9,16

的な。こうすると1群、2群がわかりやすい。

100項ぐらいぶっちゃけ数えれてしまう。。。

1

1,4

1,4,9

1,4,9,16

1,4,9,16,25

1,4,9,16,25,36

1,4,9,16,25,36,49

1,4,9,16,25,36,49,64

1,4,9,16,25,36,49,64,81

とかやって執念で数えようとしてたら、

項的には、1+2+3+4+5+6+7+8+9+10+・・・　ってなってるやん( ￣−￣)　ていいかげんバレる。。

なので

ってことになる。。

ただ、ここまでやるとちょいちょい自分が何をしているのかわからなくなるので、実際に数字を代入して我を取り戻しておくとよい。

試しにn=4とかやってみる。

すると、 なので　とりま１０。。。。　

ってなるとこやけど

1

1,4

1,4,9

1,4,9,16

の4群までの項の数は？　つったら　数えてみたら10。。　　

とわかる。

で、100項までいきたいんで適当にnをあてる。。。

n=13とかやってみると91・・・　おしい( ￣−￣)

n=14としてみると105・・・　いきすぎた( ￣−￣)

ということで14群を書いてみると

1,4,9,16,25,36,49,64,81,100,121,144,169,196

なので196が105番目やん( ￣−￣)

じゃあ81が100番目やん。。となる。。

(2)　こういうやつは最後の群だけ別でたす( ￣−￣)

どうせなんか法則あるんやろ( ￣−￣)ということで、眺めてみると・・１群あたり・・

２乗してるやつたしてるだけやん。。。 とわかる。。

100項は14群の途中なので、13群まではふつうにたせる。

ということで　　を計算する。　

14群は81までなので、

1+4+9+16+25+36+49+64+81

という感じにそこまで自力でたせばOK。

223

これもとりま縦に並べるか( ￣−￣)　っつって並べる。　解答みたいに横でもええけど、縦の方が　何群目＝何行目　ってなってわかりやすいような気がする。で、結局、1群目1こ、2群目2こ、3群目3こ・・・　ってなってるんで800項は何群かな～　ってかんじやけども。まずは実験する。

1,2,3,4,5,6,って増えていってるんで、　かな～という感じはする。　せっかく書いてくれてる12番目はというと・・・

n=3としてみると、6。

n=4としてみると、10。

12はその次ぐらいで含まれてしまいそうなんで第５群かな。。。( ￣−￣)　

上から数えてみると、　で第５群。４STEPに書かれてるのを数えてもやっぱり12番目は　でやっぱり第５群。。

つまり、12番目の項は、n=4まではMAXで使い切って10。そして残ってるのが2なので、

第５群の２番目となる。。。

当然同じ技を800にもかます( ￣−￣)

n=38としてみると741

n=39としてみると780

あと20で800になってまう( ￣−￣)

ってことは800は第４０群っすね( ￣−￣)　しかも20番目っすね。。　とわかる。。

で、和はというと、

どうせなんか法則あるんやろ( ￣−￣) とナメてとりあえず計算してみると、解答みたいにえらい単純なことになっている。。。。マジか。。。っていうぐらいにシンプルに各群の和が収まっている。。

あとは上の問題のように最後の群だけ別でたす。

224

これは初見で思いつくわけないので、ほほ～うまいね～ ( ￣−￣)

と思いながら解答を読む。。

225

（１）こいつは何を言ってるんだ？( ￣−￣) 　となりそうなことを書いてるけど結局、

と項がn個あってｘをn-1回、数字を１回使うと の項ができる。

どの数字を使うかは自由なので、

1,2,3,4,5,6,7,8,・・・n　まで使える。　だから解答みたいにシグマでたすことになる。。

(2)これは(1)と同じ考え方をすると、

xをn-2回、数字を２回使うことになる。。どの数字の組み合わせでもいいので、224番で使ったテクニックを拝借してくることになる。

226

難関大でよく見かける格子。。

これの場合はふつーに長方形を半分で、でええかな。注意点もあるので手順的には以下のようになる。

という感じ。

全体は(n+1)(3n+1)。 原点を含んでいるのでn×3nではないことに注意。よくわからない場合はn=2とかてきとうにちまっとした長方形つくって数えて検証する。

斜めの線は(3n, 0) , (0, n)を通るんで となる。

ということはxが３の倍数のときにyが整数になりそう。

ここでも小さい数で実験。

n=3とかやってみると、(9,0) , (0,3)をとおる線なので

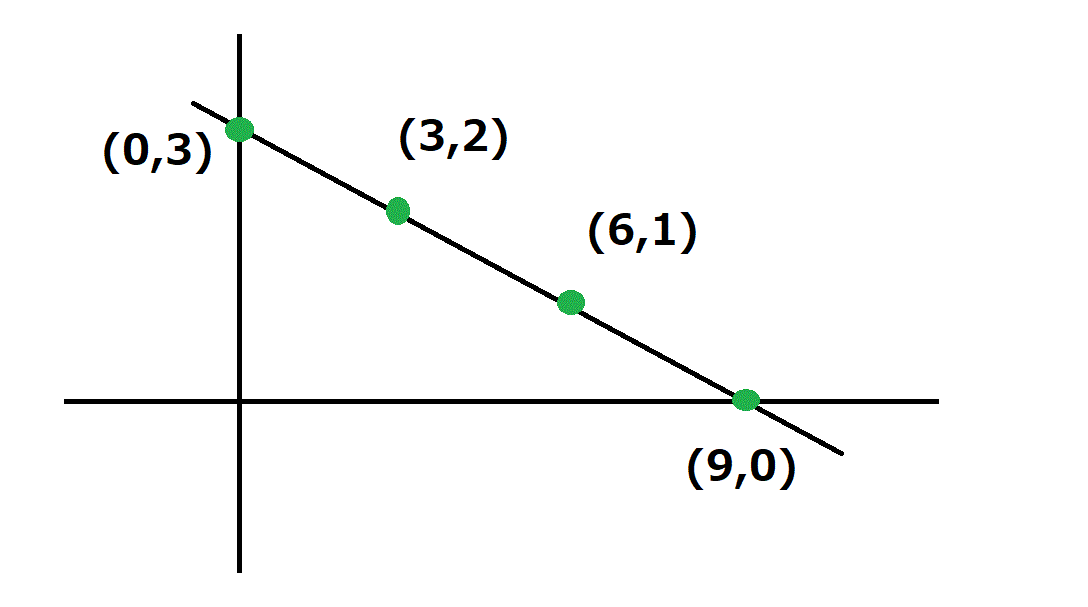
ななめの点は４つすね( ￣−￣)

もう一個データをとってみる。　n=4としてみると、

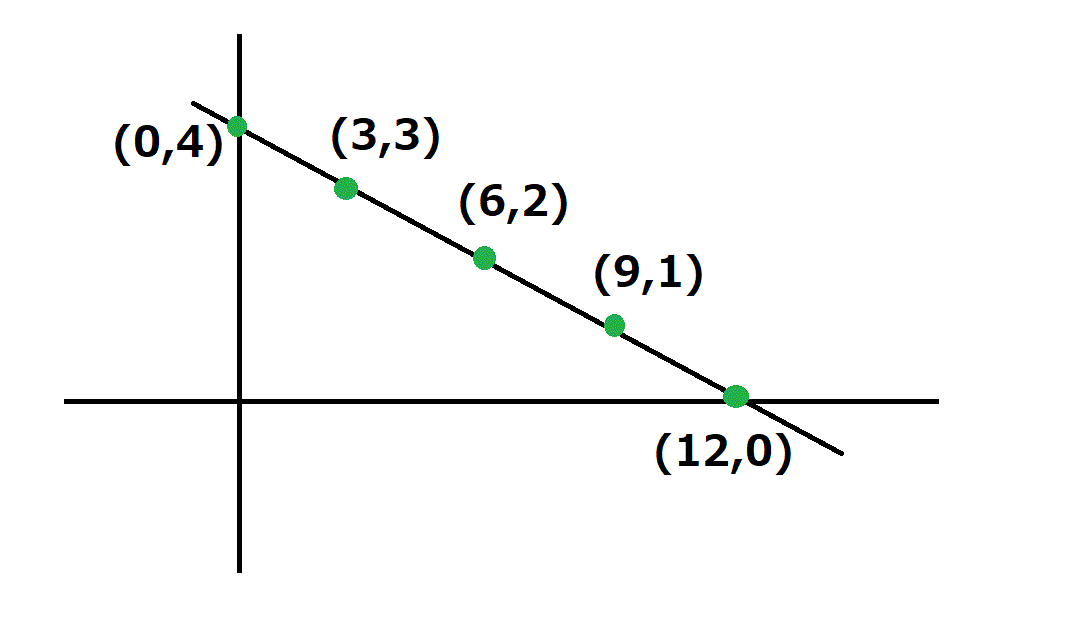
となって５つ。。。

ま～　ななめの点はn+1個で確定かな( ￣−￣)　とわかる。

ということで手順通りにやっておわり。つまり、

長方形(n+1)(3n+1)から、斜めの点(n+1)個引いて、半分にして（左下の◣だけ残す）、ななめの点(n+1)を戻す。

227

これは、かなり解答通りでええかと。。

特に付け加えるようなこともなさそう。。

x=kのところで切って、それをその線上に含まれる数を数えといて、kを０からｎまで変えていって全部たす、という方向性は積分でもよく使うので難関大を目指すならこの考え方に馴染んでおきたいところ。

228 漸化式

代入するだけ。

229

これはクソほど重要( ￣−￣)

そもそも漸化式（ざんかしきと読みたくてしょうがない。。。）は

鑑賞する気持ちでやるのがよい。

(1)　　。。ちょいいじって、

　　　。。。ほほ～( ￣−￣)

　　なにかしらの数列 に5たしたら次の数列。。。

　　 に5たしたら、　。。。。どうみても等差数列やんけ( ￣−￣)　　とわかる。

あとは等差数列の一般項に代入しておわり。　公差はみたままやし、初項も言われてる。。

(2) おなじ。

(3) これも眺めてみる。。。。

　。。。ほほ～( ￣−￣)

　なにかしらの数列 に5かけたら次の数列。。。

　 に5かけたら、 　。。。。。どうみても等比数列やんけ( ￣−￣)　　とわかる。

あとは等比数列の一般項に代入して終わり。5かけまくってるので5が公比、初項は言われてる。。。

(4) おなじ。。

これらの問題は漸化式の基本中の基本なので、決してこのへんでもたつくことのないようにやり込もう。

230

これの解答もひどいな～( ￣−￣)

ま、漸化式なのでとりま鑑賞してみる。。

(1)　 。。。ほほ～( ￣−￣)

つまり、　次のやつ から前のやつ を引いたら 2n　。。。。( ￣−￣)

　次のやつと前のやつの差が2n。。。　( ￣−￣)

　　差が数列になっている。。。。

　　　　　　。。。。　　　　。。。階差数列やん( ￣−￣)　　　とわかる。。

あとは階差数列の一般項に代入しておわり。

などという学生はもれなく 210へ帰ろう。。

(2) (3) も同じ。

(4)は207もあり。

とにかくここら辺までくると、やり込み不足が露呈してしまうので注意したい。

231

これは、数列の中で一番重要なやつといってもいいぐらいに重要なやつ。

漸化式といえばこれ。

。。。というやつ。６問全部同じやり方。場所がおかしいぐらいで、全部(1)みたいな形に持ち込めば終わり。

232

例題２４と同じく、逆数とってさばいて、最後にもとに戻す。　というだけ。

結構出てくるのでこのやり方は常備しとくとよい。

233

両辺を でわる。。と、

となってすばらしいことになる。。

あとは　 という風に見ればありがちな展開で終了♪

(2)も同じようなもん。

これもありがちなパターンなので偏差値５０以上の大学を目指すんであれば必須。

最初はいろんなパターンあるな～( ￣−￣)　って思うところやけども馴染んでくると

「わるに決まってるやん( ￣−￣)」　ってなる。

234

これは解答でいけるかな。

ただ、この流れは知っとかないと入試で困るｗ

とりあえず を作る。

そして連立。　あとは適当にいじってたら終わってる。

この が思いつかなかったら、移項とかして割ったりしていろいろいじるけど結局逃げられるｗ

235

最初、「ん？( ￣−￣)　」　ってなるところやけども、とりあえず

とおいてみるか。。。

ってやってみると、

ってなるやん。。

つまり、ある数と次の数が同じ。。　つまり、全部同じ数の数列。。。　とわかる。

(2)も分母に行ってしまってるだけで方向性は全く同じ。。。

236

に 入ってるやん。。。

ってなるところやけども解答通りに を用意してみると。。。

あっさり見慣れた漸化式になって終了♪

などという場合は　231に戻ってアホみたいに繰り返しトレーニングしよう。　231は重要な基本の形。

237

なにやら読む気にならん感じの問題。。

偏差値高めの大学を目指してるんなら、ま～ちゃんと見とこか～という感じ。

とりあえず、こんな感じ。

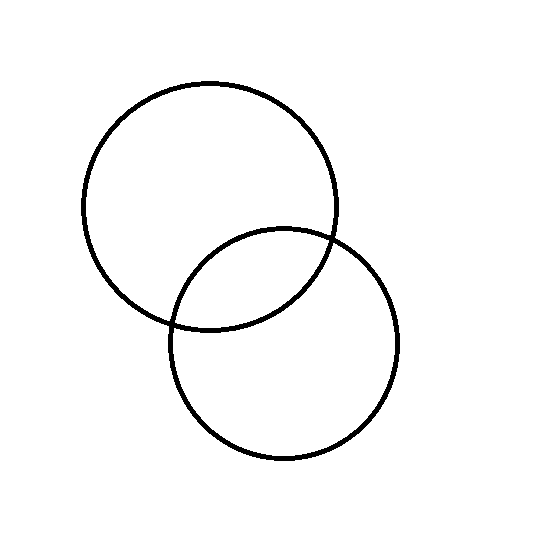
で円をここにたすと、

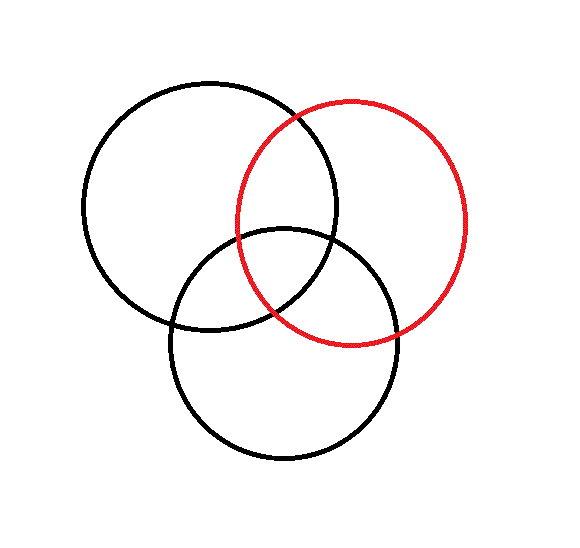
この赤い円のようになるのでこの図では4つ点がたされてる。

これを検証していくと、解答に書かれてるの漸化式になる。。

問題文が難しくて解答が簡単なパターンのやつ。

238

これはクソほど重要。

数学Ⅲの極限につながっていく問題。

１回操作すると正方形の１辺の長さが 倍になる。

なので面積的にはその２乗。

しかも最初の辺の長さは１。

このあたりの情報で数列を作っていく。

これは数学Ⅲとか入試問題にもよく出てくる典型問題なのでクソほど重要。

239

これは見慣れないと、なにこれ？　確率か？( ￣−￣)　みたいに思うところやけども、地味に東大にも通じる重要問題。偏差値が高い大学を受けるつもりなら必須。

240

これは初見だとなかなか厳しいものがあるけど、解答でわかりやすいかな。

241

ここらへんまでくると、この問題というよりはこれまでのやり込み具合がモノを言う。

この問題だけわからんてことはないやろう。。

例題のように連立っぽく解く。

242

これは解答通りで問題なさそう。

この問題みたいにふたつあるやつは、単純にたしたりするだけで終わることが多い。

なのでネタさえわかってしまえば別に難しくはない。

243

数学的帰納法のとこ。

とりあえず数学的帰納法のイメージを説明しよう。

まず、この４人がいたとする。

そして、このふたりはクソほど仲良し。なのでもし片方が犯人ならもう一人も確実に犯人。

で、この真ん中のふたりもクソほど仲良し。なのでもし片方が犯人ならもう一人も確実に犯人。

で、さらにこの右のふたりもクソほど仲良し。なのでもし片方が犯人ならもう一人も確実に犯人。

で、今、こいつが犯人として捕まった。

・・・・

じゃあ・・・( ￣−￣)

こいつら全員犯人やん( ￣−￣)　

っていう論法。

n=1のときを先にやるんで紛らわしいけども、基本は上の図のような話。

問題の解説

(1)

とりまn=1を代入して確認。

n=k のときに成り立つとして素材を作る。

n=kのとき成り立つんなら、

で、まず n= k+1 なら何になるか予想する

すると、kだったところを k+1 に変えた 　に決まっとるやん( ￣−￣)

で、あとは、ほんまに になるのかを検証すれば終わり。

n=k+1のとき、左辺を調べてみると、k+1の分ちょっと増えるので、

となって１つ最後に加わる。。

ここで、上の素材を使うと、 という風に1+10+・・・のところがすっきりする♪

そして、これをちょいいじると、

となって、当初予想した通り、 になる。

つまり、n=kで成り立つんなら、n=k+1でも成り立つ。

つまり、

左のやつが犯人ならその隣のやつも確実に犯人だと言える。

n=1とのときは最初に求めてるので

すべての自然数で成り立つ（全員犯人だ）、と言える。

(2)　も同じやり方。

244

これも↑と同じ。

数学的帰納法はとっつきにくいけど理解してしまえば、やることはかなりバレバレ。

245

246

247

248

249

４STEP解説一覧に戻る

2021年4月16日【数学4STEP】クソ解答の解説